How To Calculate Pore Size From Bet Data?

Overview of BET Analysis

BET analysis, named after its developers Brunauer, Emmett, and Teller, is a technique widely used in the field of surface area measurement. This method is pivotal in determining the specific surface area of materials by analyzing the physical adsorption of gas molecules onto a solid surface. Notably, BET analysis is predominantly applied to porous materials to understand their surface properties and porosity characteristics.

By utilizing the BET method, researchers can gather valuable insights into the surface area, pore volume, and pore size distribution of various materials. This analysis involves the quantitative assessment of the interaction between gas molecules and a solid surface, enabling the calculation of crucial parameters such as monolayer capacity and the BET specific surface area. Overall, BET analysis serves as a fundamental tool in material science and catalysis research for characterizing porous structures and understanding surface interactions.

Understanding BET Data

BET data, acquired through Brunauer-Emmett-Teller analysis, provides crucial insights into the surface area and porosity of materials. It is essential in characterizing the adsorption behavior of substances on a surface. By analyzing the specific surface area and pore size distribution, researchers can gain valuable information about the material’s properties and potential applications.

Interpreting BET data involves studying the nitrogen adsorption isotherm to understand the surface characteristics of the material. The isotherm, a plot of the amount of nitrogen adsorbed versus relative pressure, reveals vital information such as monolayer capacity and surface area. Understanding these data points allows researchers to optimize material synthesis and tailor properties for desired applications.

Importance of Pore Size Calculation

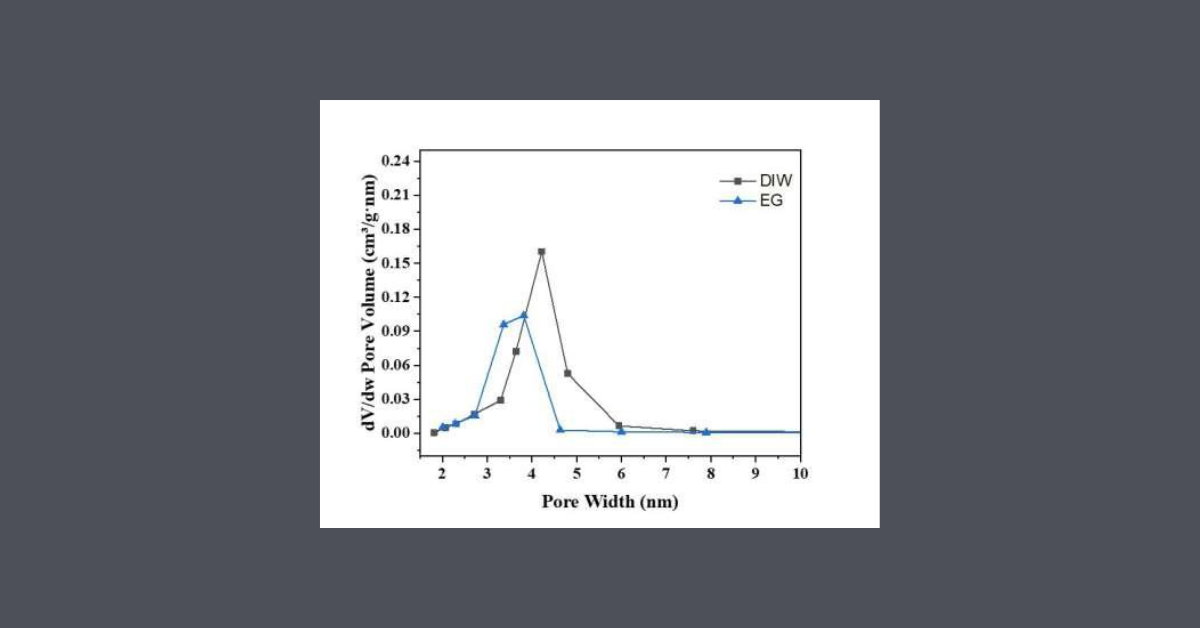
Accurately determining pore size is crucial in various fields such as material science, catalysis, and adsorption studies. The size of the pores in a material significantly influences its properties and performance. For instance, in the field of catalysis, the pore size directly impacts the surface area available for catalytic reactions, thus influencing reaction rates and efficiencies. Therefore, understanding and calculating pore size are essential for optimizing material design and performance in various applications.

Moreover, pore size calculation plays a vital role in characterizing the porosity of materials. Different pore sizes can affect the adsorption and desorption capacities of materials, making pore size analysis pivotal in determining the efficiency of gas storage, separation processes, and drug delivery systems. By accurately evaluating pore size distribution, researchers and scientists can tailor materials to enhance their specific functionalities and applications, leading to advancements in various industries.

Basic Concepts of Pore Size Calculation

When determining the pore size of a material, it is essential to understand the concept of adsorption and desorption. Adsorption refers to the process of molecules adhering to a surface, while desorption involves the release of these molecules. By analyzing the amount of gas adsorbed at different pressures, valuable insights can be gained regarding the pore structure of the material under investigation.

Another crucial concept in pore size calculation is the distinction between micropores, mesopores, and macropores. Micropores have diameters less than 2 nm, mesopores range from 2 nm to 50 nm, and macropores are larger than 50 nm. By categorizing pores based on their sizes, researchers can make informed assessments about the material’s porosity and the potential applications it may have in various industries.

Mathematical Formula for Pore Size Calculation

When it comes to determining the pore size in materials using BET analysis, a key mathematical formula used is the Kelvin equation. This equation is based on the principle of capillary condensation within porous structures, providing insight into the size of the pores by analyzing the amount of gas adsorbed at different relative pressures. By plotting the data obtained from BET analysis and applying the Kelvin equation, scientists and researchers can accurately calculate the pore size distribution within a given material.

In addition to the Kelvin equation, another important mathematical formula used in pore size calculation is the Barrett-Joyner-Halenda (BJH) method. The BJH method complements the BET analysis by focusing on the desorption branch of the isotherm data, allowing for a more detailed examination of the pore size distribution. By incorporating the data obtained through both the BET analysis and the BJH method, a comprehensive understanding of the pore structure within a material can be achieved, aiding in various applications ranging from catalysis to material science.