How To Calculate Pore Size Distribution From Bet?

Definition of BET analysis

Brunauer-Emmett-Teller (BET) analysis is a technique utilized in materials science to determine the specific surface area of porous materials. This method is named after its developers, Stephen Brunauer, Paul Hugh Emmett, and Edward Teller. BET analysis is particularly valuable in the characterization of catalysts, adsorbents, and other materials with porous structures. The fundamental principle behind BET analysis lies in the multilayer adsorption of gas molecules onto the material surface, enabling the calculation of surface area and porosity.

By conducting BET analysis, researchers can gain insights into the physical properties of porous materials, such as their pore structure and overall surface area. This technique serves as a crucial tool in evaluating the performance and efficiency of various materials in applications ranging from catalysis to gas storage. BET analysis plays a pivotal role in understanding the behavior of gases interacting with solid surfaces, offering valuable information for optimizing material design and functionality.

Importance of pore size distribution in materials science

Pore size distribution plays a crucial role in materials science as it directly impacts the physical and chemical properties of materials. Understanding the distribution of pore sizes is essential for determining the material’s porosity, surface area, and permeability. This information is vital in various applications such as determining the efficiency of catalysts, adsorbents, membranes, and other porous materials.

Furthermore, pore size distribution analysis provides insights into the performance and behavior of materials in different environments. It helps researchers and industries optimize the design and selection of materials for specific applications based on their pore structure characteristics. By accurately characterizing the pore size distribution, scientists can tailor materials to meet desired performance criteria, leading to advancements in fields such as energy storage, environmental remediation, and drug delivery systems.

Understanding the BET equation

The BET equation, developed by Brunauer, Emmett, and Teller, is a fundamental tool in understanding the adsorption of gas on solid surfaces. It relates the quantity of gas adsorbed on a material to the relative pressure of the gas in the surrounding atmosphere. The equation assumes that the surface of the material is energetically homogeneous and that a monolayer of gas molecules forms on the surface.

The BET equation can be expressed as: (V\_m\*(P/(1-(P/P\_0))) = (V\_m\*(C-1))\*((1/(P\_0))+(C-1)/P\_0\*P) where V\_m is the volume of gas adsorbed at the monolayer coverage, P is the relative pressure of the gas, P\_0 is the saturation pressure of the gas, and C is a constant related to the energy of adsorption. By fitting experimental data to the BET equation, researchers can extract valuable information about the specific surface area and the distribution of pore sizes in a material.

Step-by-step guide to calculating pore size distribution from BET data

*Analysis of BET data plays a crucial role in determining the pore size distribution of materials. The first step in this process involves plotting the adsorption isotherm data in a specific format, typically using the BET equation. Next, the surface area of the material is calculated by fitting the data to the BET equation, which helps in understanding the monolayer coverage on the material’s surface.*

*After determining the surface area, the pore volume is calculated based on the amount of gas adsorbed at high relative pressures. By analyzing the slope of the isotherm at high pressures, one can extrapolate the volume of gas adsorbed onto the material, leading to the final step of calculating the pore size distribution. Utilizing this data, researchers can gain valuable insights into the structural characteristics of the material, enabling them to make informed decisions regarding its application in various fields.*

Interpreting the results of pore size distribution analysis

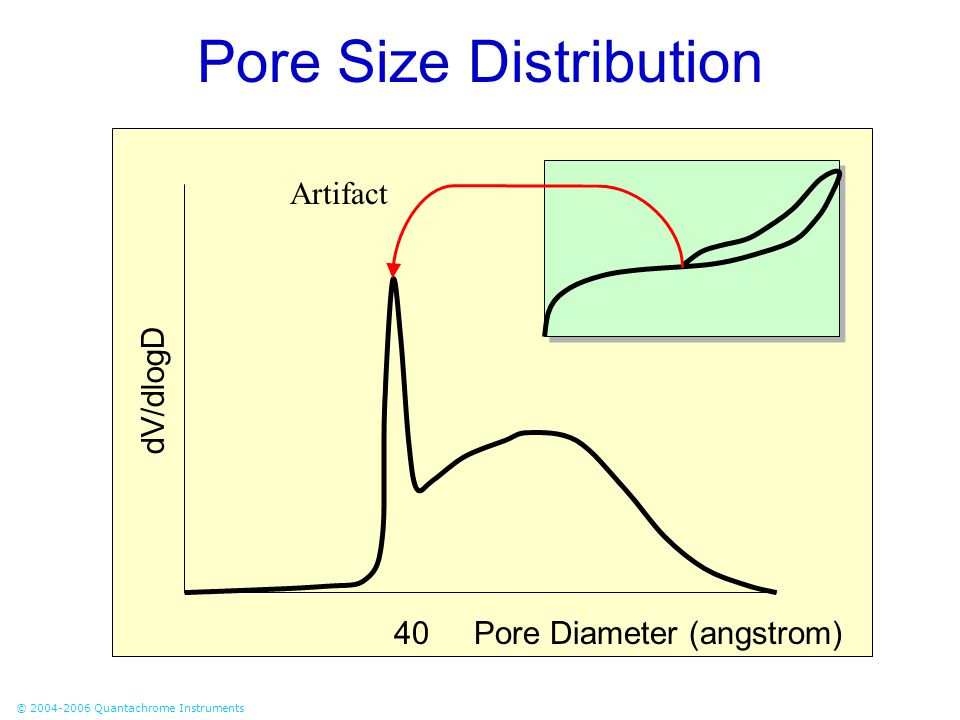
The results obtained from pore size distribution analysis play a crucial role in understanding the characteristics of materials in the field of science and engineering. By analyzing the distribution of pore sizes within a material, researchers can gain valuable insights into its properties such as surface area, adsorption capacity, and permeability. The pore size distribution curve provides information on the different pore sizes present in the material and their respective volumes, which can be indicative of the material’s performance in various applications.

Interpreting the results of pore size distribution analysis involves carefully examining the shape and characteristics of the curve. For instance, a bimodal distribution with two distinct peaks indicates the presence of different types of pores within the material. The location of the peaks on the curve signifies the dominant pore sizes present, while the area under the curve reflects the total pore volume. Researchers can use this information to optimize the material for specific applications or to compare different materials based on their pore structure.